MATERI LINGKARAN

      A.    Definisi Lingkaran

Perhatikan gambar lingkaran di atas ! 

Sebuah lingkaran mempunyai beberapa unsur, diantaranya jari – jari dan pusat lingkaran.

O merupakan titik pusat.

OA, OB , dan OC adalah jari – jari .

Jari – jari (r) pada lingkaran memiliki panjang yang sama. Sehingga, OA = OB = OC.

Lingkaran adalah tempat kedudukan titik – titik (himpunan titik) yang jaraknya terhadap satu titik tertentu adalah  sama ( konstan ). Titik tertentu disebut pusat lingkaran,dan  jarak konstan disebut jari – jari lingkaran.

      B.    Jarak Antara Dua Titik

Sebelum memasuki persamaan lingkaran, diperlukan penguasaan terlebih dahulu mengenai jarak dua titik. Dengan menggunakan Theorema Phytagoras, kita dapat menemukan jarak antara dua titik (d) yaitu dengan pemisalan titik A (x₁,y₁) dan B (x₂,y₂,) .

Dengan menggunakan definisi lingkaran dan mencari jarak antara dua titik tersebut, diharapkan siswa dapat menemukan rumus persamaan lingkaran dengan pusat O(0,0) dan jari – jarinya r.

      

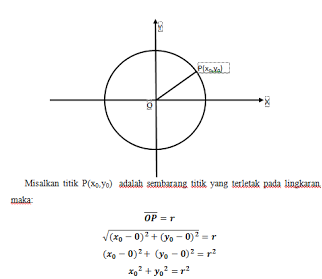
      C.    Persamaan Lingkaran dengan Pusat O(0,0) dan jari–jari r

Untuk memudahkan penulisan rumus, kita dapat menghilangkan indeks 0 pada  x₀ dan y₀, sebab maknanya akan sama saja. Sehingga akan menjadi .

Jadi , persamaan lingkaran dengan pusat O(0, 0) dan jari-jari r adalah :

x² + y² = r²

      

      D.    Persamaan Lingkaran dengan Pusat M(a,b) dan jari–jari r

    

 Contoh Soal

      E.    Bentuk Umum Persamaan Lingkaran

Dengan menggunakan persamaan lingkaran dalam bentuk umum, siswa dapat menemukan pusat dan jari – jari lingkaran, dengan cara sebagai berikut :

Persamaan Lingkaran:   

Contoh Soal

       

      

       F. Kedudukan Titik Terhadap Lingkaran

Contoh 5

      

      G.    Kedudukan Garis Terhadap Lingkaran

Secara geometri ada tiga kedudukan garis terhadap lingkaran, yaitu :

Contoh

Tentukan posisi garis y = 3x + 2 terhadap L  x² + y² + 4x – y + 1 = 0 !

Jawab :

Subtitusi garis y = 3x + 2 ke L  x² + y² + 4x – y + 1 = 0, diperoleh:

            x² + (3x + 2)² + 4x – (3x + 2) + 1 = 0

            10x² + 13x + 3 = 0 sehingga nila a = 10, b = 13 dan c = 3

Nilai D = b² – 4ac = 169 – 4.10.3 = 49 > 0

Karena diperoleh D > 0 maka garis y = 3x + 2 memotong ligkaran L di dua titik yang berlainan.

     H.    Jarak Titik Pada Lingkaran

      1.      Titik di luar lingkaran

       

2. Titik di dalam lingkaran